Use L1 and L2 Norm as parameter Regularization
L1 Norm as Regularization
| $ J(h(\theta, X), y) + \lambda* | \theta | $ |
L2 Norm as Regularization
$J(h(\theta, X), y) + \lambda* (\theta)^2$
Here, $J$ is a loss function, $h$ is a model function, $\theta$ is parameter, $X$ is feature, $y$ is target, and $\lambda$ is hyperparameter where adjust how much to regularize.
Or use both of them, which is elastic net.
Why L1 is always doing a better job introduce sparsity to $\theta$ ? It always troubles me. And I have searched for answers. and most of the time, people are telling you, it’s because of the speed of change differs between L1 and L2 when $\theta$ is really small.
Like this graph here.
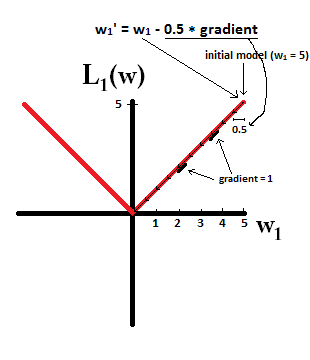
And this graph here.
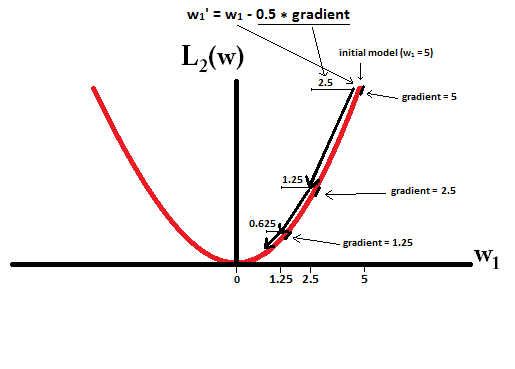
But it is just not intuitive too me, maybe it is to most of people.
From this graph for sure I can tell that the $w$ ,which is $\theta$ in our equation, changes way faster in L1 when it get smaller. But sparsity means it stays at the very button. Both of the updating equation in the graph doesn’t guarantee you that once you have $w$ = 0, you won’t move out of zero.
Why the chance of obtaining a zero in $w$ have something to do with the speed of changing ?
So, i decide to take a step back. By asking myself, what does it mean to have better sparity?
The implicit prior is that, we have two model both fitted/converged. Then we can compare the sparsity. The further prior is that, we have sparity in the true model -> we have redundancy within features.
But then.. it’s still by chance. but definitely not ture in my coding experience, not matter when i have a l1 normed model, there will be 0s. even if there is no redundancy.